Frequently Asked Questions: transmissie en maatregelen
- Is de situatie bij het begin van de tweede golf wel gelijkaardig aan die bij het begin van de eerste golf in het begin van maart? Er wordt nu toch veel meer getest dan het geval was toen.
- Hoe werd de drempelwaarde van 20 gevallen op 100,000 inwoners bepaald? Het is niet logisch dat een gemeente met slechts een beperkt aantal gevallen meteen donkerrood kleurt.
- Is het gebruik van mondmaskers nuttig tijdens het wandelen of joggen op verlaten plaatsen?
- Wordt een tweede golf van COVID-19 besmettingen niet gedreven door een groot aantal vals positieven in combinatie met een toename in het aantal testen? (Op basis van een tekst van Kurt Barbé)
- Waarom zijn er verschillende reproductiegetallen?
- Zal het SARS-CoV-2 virus spontaan verdwijnen zodat we ons eigenlijk minder zorgen moeten maken?
- Kan het viraal materiaal van het coronavirus binnendringen in het DNA van de cel?
- Waarom kon men in 2009 wel op enkele maanden tijd een vaccin klaar hebben tegen het H1N1 influenza virus (de “Mexicaanse griep”) en duurt het nu zeker anderhalf jaar voor er een vaccin is tegen SARS-CoV-2?
Is de situatie bij het begin van de tweede golf wel gelijkaardig aan die bij het begin van de eerste golf in het begin van maart? Er wordt nu toch veel meer getest dan het geval was toen.
Het klopt inderdaad dat het aantal gedetecteerde gevallen kan stijgen in functie van het aantal testen dat wordt uitgevoerd. Het is dus belangrijk om te corrigeren voor het aantal testen dat daadwerkelijk wordt uitgevoerd. In het begin van maart was de gevalsdefinitie nauwer, hetgeen impliceert dat toen minder mensen zich konden laten testen en veeleer deze met ernstige symptomen (met uitzondering van zorgpersoneel en terugkerende reizigers met milde symptomen). Bijgevolg werden enkel de zeer ernstige gevallen gevonden, terwijl COVID-19 wijdverspreid was in de Belgische populatie. Vandaag wordt er breder (volgens een andere gevalsdefinitie) en meer (niet noodzakelijk voor mensen met symptomen om diverse redenen) getest waardoor een groter aantal asymptomatische en milde gevallen terechtkomen in de dagelijks gerapporteerde bevestigde gevallen. Dat gezegd zijnde, zijn er een aantal belangrijke argumenten die een kordate en snelle aanpak, gereflecteerd in de maatregelen genomen door de federale en provinciale overheden, vereisten. In de eerste plaats zitten we sinds eind juni in een situatie waarin de gevalsdefinitie en het testbeleid ongewijzigd bleven, waardoor een toename in het aantal gevallen wijst op een toename in (lokale) transmissie (ook na nieuwe introductie van het virus door reizigers), hetgeen ook wordt waargenomen in de evolutie van het reproductiegetal $R_t$ over de tijd https://gjbex.github.io/DSI_UHasselt_covid_dashboard/. Bovendien nemen geschikte modellen voor kortetermijnvoorspellingen de positieve test ratio (d.i. de verhouding van het aantal positieve testen op het totaal aantal uitgevoerde testen) in rekening, waarbij expliciet wordt gecorrigeerd voor een verandering in testbeleid in vergelijking met de eerste golf van maart-april 2020. Andere modellen doen dit niet en veronderstellen dus impliciet dat een toename in aantal bevestigde gevallen rechtstreeks gerelateerd is aan een toename in echte gevallen, en dat het testbeleid over de beschouwde periode dus ongewijzigd bleef. Het Belgische beleid werd mede geïnformeerd door modellen die wel rekening hielden met de veranderde testpraktijken. Let wel, zelfs indien de positieve test ratio wordt gebruikt, dienen we voorzichtig te zijn wat betreft interpretatie. Enerzijds worden sommige groepen vaak meerdere keren getest (bv. gezondheidsmedewerkers dienen een tweede test te laten afnemen na een eerste negatieve test). Anderzijds is de geteste populatie geen willekeurige populatie en is de reden van testafname gewijzigd over de tijd.
Gelukkig, dankzij een meer actief testbeleid, hebben we bij het ontstaan van de tweede golf veel eerder kunnen ingrijpen dan bij de eerste, en zullen we hopelijk dan ook niet enkel minder verregaande maatregelen kunnen handhaven, maar deze ook sneller weer kunnen afbouwen. Niettemin was een doortastend ingrijpen op basis van de evolutie van $R_t$ gerechtvaardigd. We willen immers niet belanden in de situatie van begin maart waarin een algemene lockdown noodzakelijk was om de situatie beheersbaar te houden voor ons gezondheidssysteem.
Hoe werd de drempelwaarde van 20 gevallen op 100,000 inwoners bepaald? Het is niet logisch dat een gemeente met slechts een beperkt aantal gevallen meteen donkerrood kleurt.
Het werken met een relatief cijfer, zoals het aantal gevallen per 100,000 inwoners in dit geval, geeft een meer correcte en meer objectieve vergelijking van de besmettingsgraad tussen verschillende gemeenten. Een absoluut aantal gevallen kan zeer misleidend zijn, omdat dan grote gemeenten met veel inwoners mogelijks meer gevallen hebben, enkel omdat hun inwonersaantal groter is dan dat van andere gemeenten. Echter, het werken met relatieve aantallen kan leiden tot een zeer groot aantal gevallen per 100,000 inwoners voor kleine gemeenten met slechts enkele bevestigde gevallen. Statistisch gezien gaan we hiervoor corrigeren (technisch heet dat ‘smoothing’) door de incidenties van zulke gemeenten uit te middelen door ook de gegevens van de omringende gemeenten mee te beschouwen. Op die manier krijg je een beter beeld van de ernst van de situatie en houdt je rekening met de gevallen in een gebied, en niet alleen maar het aantal gevallen in één enkele gemeente. Zulke smoothing technieken staan centraal in ruimtelijke data analyse en small area estimation (Gelfand et al., 2010; Lawson, 2018), ook gekend van bijvoorbeeld straling rond een nucleaire site, enz. (zie https://gjbex.github.io/DSI_UHasselt_covid_dashboard/).
De drempelwaarde van 20 gevallen per 100,000 inwoners is pragmatisch gekozen, maar de keuze van een dergelijke drempelwaarde is voornamelijk nuttig om trends in het aantal nieuwe gevallen in de gaten te houden en eventueel van daaruit besluitvorming te ondersteunen. Idealiter worden verschillende drempelwaarden gekozen en trends in functie hiervan bekeken.
Referenties:
- Lawson, A.B. (2018). Bayesian Disease Mapping: Hierarchical Modeling in Spatial Epidemiology. Chapman & Hall/CRC; Boca Raton. Gelfand, A., Diggle, P.J., Fuentes, M., Guttorp, P. (2010). Handbook of spatial statistics. Chapman & Hall/CRC Handbooks of Modern Statistical Methods; Boca Raton.
Is het gebruik van mondmaskers nuttig tijdens het wandelen of joggen op verlaten plaatsen?
De waarde van het gebruik van mond-neusmaskers in de gezondheidszorg werd reeds duidelijk aangetoond (zie, bv., WHO, 2020). Daarom moeten zorginstellingen voorrang krijgen in geval van tekorten aan persoonlijke beschermingsmiddelen (PBM’s), zoals in de eerste weken en maanden van de pandemie. Indien deze tekorten zich in de (nabije) toekomst opnieuw voordoen, moet opnieuw voorrang gegeven worden aan zorgverleners.
Echter, gezien het toenemende bewijs van de rol van pre- en asymptomatische overdracht in de huidige COVID-19-pandemie (ECDC, 2020; Ganyani, 2020; Howard, 2020), is het gebruik van universele mond-neusmaskers als preventieve maatregel voor de algemene bevolking onder toenemende aandacht gekomen van verschillende beleidsmakers. Dit betreft het gebruik van zowel chirurgische als doe-het-zelf-maskers, gemaakt van verschillende stoffen (mede ingegeven door een tekort aan PBM’s in de eerste golf van de epidemie in maart-april 2020). Het effect van chirurgische maskers voor de verspreiding van micro-organismen werd reeds uitvoerig aangetoond voor verschillende infecties in een gecontroleerde omgeving (Zuckerman et al., 2009; Dharmadhikari et al., 2012; Milton et al., 2013; Vanden Driessche et al., 2015). Hoewel er bewijs is dat maskers ook in de gemeenschap het transmissie-risico kunnen verminderen (in een orde van grootte van ~15%), moet ‘gemeenschap’ echter duidelijk worden gedefinieerd. Het gaat hier over gesloten publieke ruimten (bv. openbaar vervoer, winkels) en open publieke ruimten waar de afstand niet kan worden gewaarborgd (bv. drukke winkelstraten) (MacIntyre and Hasanain, 2020; Lye and Wehby, 2020, Mitze and Wälde, 2020). Het is duidelijk dat het dragen van maskers in openlucht, tijdens het wandelen of fietsen op verlaten plaatsen, simpelweg geen extra bescherming oplevert wanneer een fysieke afstand van 1,5 m wel kan worden gerespecteerd (Chu et al., 2020). Daarenboven is het dragen van een mond-neusmasker tijdens het sporten, niet enkel onzinnig omdat het masker onmiddellijk verzadigd is en dus niet werkt, het kan ook tot duizeligheid bij de sporter leiden (Gezondheid en Wetenschap, 2020). Bovendien heeft het een ontradend effect om te sporten, terwijl sporten erg belangrijk is voor onze mentale en fysieke gezondheid.
Kortom, het gebruik van mond-neusmaskers is slechts zinvol in twee situaties:
- Binnen: in gesloten publieke ruimten zoals op de trein/tram/bus, in de winkel of op de werkvloer,
- Buiten: wanneer de fysieke afstand van 1,5 m niet kan worden gerespecteerd. Dus waar het druk is of waar je verwacht dat het druk kan zijn. Het is zoals met het verkeersreglement: ook daar moet de bestuurder drukte juist kunnen inschatten, of snelheid aanpassen aan de weersomstandigheden. Zo zal de burger nu het dragen van een mondmasker moeten kunnen laten afhangen van de drukte van de plek, binnen en buiten.
Als laatste moet worden benadrukt dat het gebruik van een mond-neusmasker niet als een op zichzelf staande maatregel kan worden beschouwd. Afstand houden geldt altijd als regel nummer één, aangevuld met adequate ventilatie van gesloten ruimtes, regelmatig handen wassen (lees: handschoenen hebben geen zin), zelfisolatie gedurende 7 dagen in geval van symptomen en quarantaine gedurende 14 dagen bij risicocontact.
Referenties:
- World Health Organization (WHO) (2020). https://www.who.int/publications/i/item/advice-on-the-use-of-masks-in-the-community-during-home-care-and-in-healthcare-settings-in-the-context-of-the-novel-coronavirus-(2019-ncov)-outbreak
- European Centre for Disease Prevention and Control (ECDC) (2020). https://www.ecdc.europa.eu/en/covid-19/latest-evidence/transmission
- Ganyani, T. et al. (2020). Estimating the generation interval for coronavirus disease (COVID-19) based on symptom onset data, March 2020. Eurosurveillance, 25(17): 2000257. doi:10.2807/1560-7917.ES.2020.25.17.2000257
- Howard, J. et al. (2020)/ Face Masks Against COVID-19: An Evidence Review. Preprints 2020, 2020040203 (doi: 10.20944/preprints202004.0203.v1).
- MacIntyre, C.R. and Hasanain, S.J. (2020). Community universal face mask use during the COVID 19 pandemic - from households to travellers and public spaces. Journal of Travel Medicine, 27(3): taaa056. https://academic.oup.com/jtm/article/27/3/taaa056/5822103
- Mitze, T. et al. (2020). Face Masks Considerably Reduce COVID-19 Cases in Germany: A Synthetic Control Method Approach. IZA DP No. 13319 . The IZA Institute of Labor Economics, Germany, June 2020. https://www.iza.org/publications/dp/13319/face-masks-considerably-reduce-covid-19-cases-in-germany-a-synthetic-control-method-approach
- Lye, W. and Wehby, G.L. (2020). Community Use Of Face Masks And COVID-19: Evidence From A Natural Experiment Of State Mandates In The US. Health Affairs, 39(8): 1419-1425. https://www.healthaffairs.org/doi/pdf/10.1377/hlthaff.2020.00818
- Chu, D.K. et al. (2020). Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: a systematic review and meta-analysis. The Lancet, 395. https://www.thelancet.com/action/showPdf?pii=S0140-6736%2820%2931142-9
- Gezondheid en wetenschap (2020). Is het zinvol om een masker te dragen tijdens sporten? https://www.gezondheidenwetenschap.be/gezondheid-in-de-media/is-het-zinvol-om-een-masker-te-dragen-tijdens-sporten
- Dharmadhikari, A.S. et al. (2012). Surgical face masks worn by patients with multidrug-resistant tuberculosis: impact on infectivity of air on a hospital ward. American Journal of Respiratory and Critical Care Medicine, 185:1104-1109.
- Milton, D.K. et al. (2013). Influenza virus aerosols in human exhaled breath: particle size, culturability, and effect of surgical masks. PLoS Pathogens, 9:e1003205.
- Vanden Driessche, K. et al. (2020). Surgical Masks Reduce Airborne Spread of Pseudomonas aeruginosa in Colonized Patients with Cystic Fibrosis. American Journal of Respiratory and Critical Care Medicine, 192. https://doi.org/10.1164/rccm.201503-0481LE.
- Zuckerman, J.B. et al. (2009). Bacterial contamination of cystic fibrosis clinics. Journal of Cystic Fibrosis, 8:186-192.
Wordt een tweede golf van COVID-19 besmettingen niet gedreven door een groot aantal vals positieven in combinatie met een toename in het aantal testen? (Op basis van een tekst van Kurt Barbé)
In een recente studie van Kucirka et al. (2020), met een herbevestiging van de bevindingen door Mayers en Bakers (2020), werd het onderscheidingsvermogen van de RT-qPCR test onderzocht. Hierin werd aangetoond dat 2.3% van de positief geteste personen geen COVID-19 hadden opgelopen (vals positieven), terwijl het percentage vals negatieve individuen 38% bedroeg. Echter, zowel het percentage vals positieven als vals negatieven wordt sterk beïnvloed door de manier van afname en het moment waarop men test en dit in relatie tot het tijdstip van infectie of het begin van symptomen. Idealiter test men 2 tot 4 dagen na het ontstaan van symptomen (= dag 7 tot 9 na blootstelling aan het virus), wanneer het percentage vals negatieven ongeveer 22% bedraagt (zie onderstaande figuren voor de relatie tussen percentage vals negatieven en positieven en de tijd sinds blootstelling - stippellijn geeft de gemiddelde incubatietijd weer, dit is de tijd tot het ontstaan van symptomen na blootstelling aan het virus).
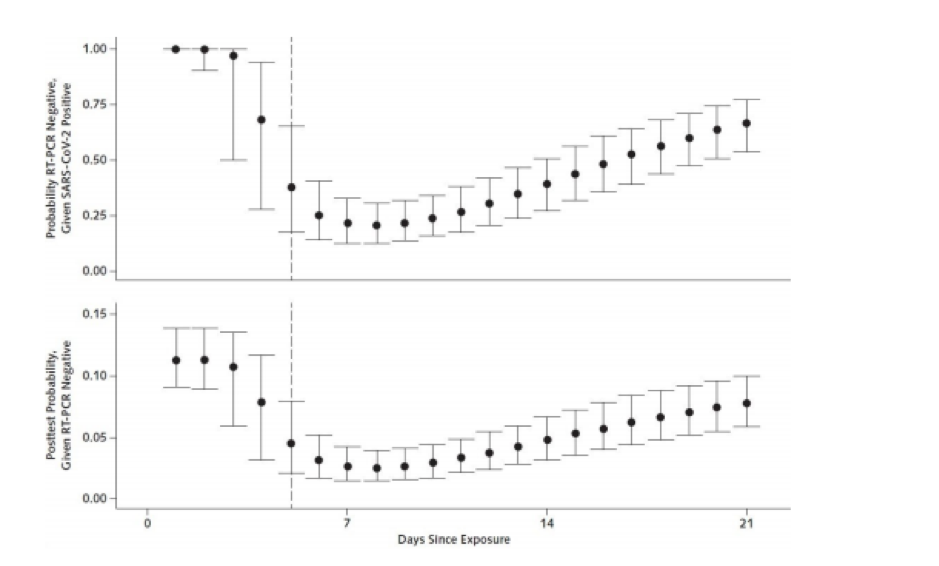
In het begin van de eerste golf, wanneer onvoldoende testmateriaal beschikbaar was, was het aantal vals negatieven hoog omdat er een lange wachttijd was, weergegeven door de stijgende curve vanaf dag 7 in de bovenstaande grafiek. Het percentage vals positieven in het aantal bevestigde gevallen is relatief klein in verhouding tot het aantal vals negatieven, waarbij vooral de laatste categorie problematisch is voor de volksgezondheid, omdat mensen dan besmettelijk zijn zonder het te weten (want de test was negatief).
Het is inderdaad correct dat meer testen kan leiden tot het detecteren van meer besmette personen (zie boven), maar deze verhoging in positieve testen dient in verhouding te worden geplaatst tot de toename in testen. Vandaar dat men de positieve test ratio (aantal positieve tests gedeeld door het totaal aantal tests) bekijkt om de situatie te evalueren. Dit dient ook te worden opgenomen op het dashboard van Sciensano. Slechts een stijging in positieve test ratio is een indicatie dat de epidemie opnieuw aantrekt en transmissie in de populatie plaatsvindt.
Referenties:
- Kucirka, L.M. et al. (2020). Variation in False-Negative Rate of Reverse Transcriptase Polymerase Chain Reaction-Based SARS-CoV-2 Tests by Time since Exposure. Annals of Internal Medicine, 13: M20-1495. doi:10.7326/M20-1495.
- Mayers, C. and Bakers, K. (2020). Impact of false-positives and false-negatives in the UK’s COVID-19 RT-PCR testing programme. Technical report.
Waarom zijn er verschillende reproductiegetallen?
Men spreekt soms van het basis reproductiegetal $R_0$ en het effectief reproductiegetal $R_t$. Het basis reproductiegetal geeft het gemiddeld aantal geïnfecteerde personen aan die één enkele geïnfecteerde persoon besmet gedurende zijn of haar hele besmettelijke periode, in een volledig vatbare populatie. $R_0$ is daarom een maat om de besmettelijkheid van een ziekte uit te drukken op het moment dat de volledige populatie vatbaar is voor infectie, en er geen maatregelen zijn genomen om verspreiding in te dijken. Het reproductiegetal hangt in essentie af van drie zaken: (1) de gemiddelde duur van besmettelijkheid, (2) het aantal contacten dat vatbaren met geïnfecteerden hebben (voornamelijk afhankelijk van hun respectievelijke leeftijden) en (3) de kans op transmissie, gegeven zo een contact. Naarmate een infectieziekte zich verspreidt in een populatie, worden steeds meer mensen eraan blootgesteld, en bijgevolg groeit de groep mensen die minstens tijdelijk niet meer vatbaar zijn voor infectie. Ook in geval van vaccinatie, kunnen gevaccineerden (tijdelijk) niet langer vatbaar zijn. M.a.w. het aantal contacten dat vatbaren met geïnfecteerden kunnen hebben evolueert, en bijgevolg verandert het reproductiegetal. Het effectieve reproductiegetal $R_t$ brengt net deze veranderende vatbaarheid in rekening, bovenop de elementen dewelke $R_0$ reeds in rekening brengt. De drie hoger genoemde elementen die het reproductiegetal bepalen kunnen eveneens veranderen over de tijd (al dan niet na attenuatie van het virus, vrijwillige gedragsaanpassingen en/of interventies, bv. 1,5m, mondmaskers, isolatie). Daarom besuderen we best het effectief reproductiegetal, het gemiddeld aantal nieuwe geïnfecteerde mensen door één geïnfecteerde persoon besmet op tijdstip t (waarbij t > 0). Wanneer $R_t$ groter is dan de drempelwaarde één, bijvoorbeeld $R_t$ = 2, dan zullen 400 besmette mensen voor 800 besmettingen zorgen, deze 800 mensen voor gemiddeld 1600 nieuwe infecties, vervolgens 3200 nieuwe gevallen, 6400 nieuwe gevallen, enz. Dan gaat het snel: de zogeheten exponentiële fase. Indien $R_t$=1, dan zullen 400 geïnfecteerde mensen op hun beurt gemiddeld 400 personen besmetten, die op hun beurt gemiddeld ook weer 400 mensen zullen besmetten, enz. De epidemie bevindt zich in een stabiel evenwicht, m.a.w. er komt een constant aantal nieuwe besmettingen bij in elke generatie van nieuwe gevallen. Om de epidemie te stoppen dienen we $R_t$ kleiner dan één te krijgen. Indien $R_t$=0.5, dan zullen 400 mensen gemiddeld 200 mensen besmetten, die dan weer opnieuw 100, dan 50, dan 25, enz. mensen zullen besmetten in opeenvolgende generaties van nieuwe gevallen. Als gevolg hiervan verliest de epidemie kracht en stopt (in afwezigheid van factoren die het reproductiegetal opnieuw doen stijgen, bijv. importatie na reizen, een toename in aantal (onbeschermde) contacten, enz.). Infectieziektentheorie leert ons dat, bij een immuniserende pathogeen, en in afwezigheid van maatregelen, deze exponentiële fase uiteindelijk op natuurlijke wijze tot een einde komt doordat onvoldoende mensen nog vatbaar zijn, en dus $R_t$<1. Echter voor heel wat pathogenen, waaronder SARS-CoV-2, kan dit gepaard gaan met heel veel ziektegevallen en een grote druk op het gezondheidssysteem.
Een andere optie is, zoals we kennen uit de eerste golf, te gaan voor “flatten the curve” waarbij we maatregelen nemen om $R_t$ te verkleinen door ons gedrag aan te passen (of in extreme vorm over te gaan op een lockdown-scenario) om de exponentiële groei te stoppen.
Het is dus nuttig om $R_t$ te schatten, als één van de vele tools om de epidemie te monitoren. Het schatten van het (effectief) reproductiegetal gebeurt op basis van verschillende veronderstellingen en databronnen. Bij een virus zoals SARS-CoV-2 is het probleem dat we simpelweg niet alle besmettingen kennen, hetgeen de bepaling van $R_t$ bemoeilijkt. Bijvoorbeeld, in maart 2020, vonden we waarschijnlijk maar ongeveer 2,5 tot 3% van alle besmettingen. Zeker de mensen zonder of met milde symptomen bleven onder de radar. Omdat er weinig getest werd, was het aantal bevestigde besmettingen geen betrouwbare indicator voor de mate waarin transmissie in de populatie plaatsvond. We volgden de epidemiologische situatie op via het aantal COVID-19 gerelateerde hospitalisaties, het aantal bedden ingenomen op intensieve zorgen, en het aantal overlijdens en schatten het reproductiegetal $R_t$ op basis van het aantal hospitalisaties. Het was de best mogelijke manier om deze belangrijke epidemiologische parameter te schatten. Echter, vandaag is het testbeleid anders: er wordt veel getest, testen staan goed op punt, er is veel testcapaciteit (al kan dit in zwaar getroffen steden en gebieden tijdelijk toch onder druk komen). Het voordeel van nieuwe gevallen te gebruiken, in plaats van hospitalisaties, is vooral dat daardoor tijd gewonnen wordt: we zien een mogelijke stijging (of daling) in het reproductiegetal sneller en kunnen sneller bijsturen indien de epidemie aan kracht wint. Hospitalisaties kunnen immers nog een hele periode stabiel blijven, zelfs wanneer het aantal gevallen al (snel) toeneemt. Dat is zeker zo wanneer er een toename in besmettingen plaatsvindt bij jongeren (die relatief zelden in het ziekenhuis moeten worden opgenomen), maar niet of weinig bij ouderen.
In die zin is het een meerwaarde, specifiek voor deze epidemie, om $R_t$ te bepalen (schatten) zowel op basis van hospitalisaties als op basis van nieuwe bevestigde gevallen: $R_{(t,hosp)}$ en $R_{(t,cases)}$. Het is dus niet zo dat één van beide schattingen juist en de andere fout is; ze brengen elk specifieke en belangrijke informatie naar voren. Als $R_{(t,cases)}$ stijgt maar $R_{(t,hosp)}$ niet, wijst dat erop dat het aantal hospitalisaties de besmettingen (nog) niet volgt, bijvoorbeeld omdat ouderen relatief weinig besmet geraken. Het omgekeerde kan ook: de epidemie kan sterk aan kracht afnemen, waardoor $R_{(t,cases)}$ daalt, terwijl ze nog kan toenemen in de woonzorgcentra. De bewoners van woonzorgcentra kunnen een relatief kleine fractie van het aantal besmettingen voor hun rekening nemen, maar een heel grote fractie van het aantal ziekenhuisopnames en overlijdens. Zoiets zal zich dan vertalen in een stijgende $R_{(t,hosp)}$.
Tot slot, bestaan er ook (wiskundige en/of statistische) modellen om een inschatting te maken van het werkelijke aantal nieuwe gevallen, al dan niet bevestigd, die eveneens kunnen gebruikt worden om $R_t$ te schatten. Deze berekeningen zijn wiskundig ingewikkelder, maar zijn desalniettemin een zinvolle aanvulling.
Een extra woordje uitleg
Er bestaan verschillende methoden om het reproductiegetal te schatten. Idealiter gebeurt dit op basis van het aantal besmettingen in de populatie. In de SIMID groep maken we gebruik van een zogeheten renewal equation aanpak volgens de methode zoals gepubliceerd in Cori et al. (2013) en rekening houdend met o.a. weekend delays en onder-rapportering (Azmon et al., 2013). Deze aanpak berekent een “backward” reproductiegetal door terug te kijken in de tijd. Naast een berekening op basis van het aantal besmettingen, kan eveneens gebruik gemaakt worden van het aantal hospitalisaties (zie dashboard Sciensano) of het aantal sterfgevallen. Het voordeel van de laatste twee databronnen is het feit dat deze vaak accurater worden gerapporteerd, maar bij kleinere waarden een grote onzekerheid met zich meebrengen. Andere verschillen tussen het gebruik van verschillende databronnen werden hierboven reeds besproken. Een overzicht van wat het reproductiegetal ons kan en vooral ook niet kan vertellen met betrekking tot de huidige COVID-19 pandemie kan je hier vinden: https://www.nature.com/articles/d41586-020-02009-w.
Referenties:
- Cori, A., et al. (2013). A new framework and software to estimate time-varying reproduction numbers during epidemics. American Journal of Epidemiology, 178(9):1505-1512. https://academic.oup.com/aje/article/178/9/1505/89262.
- Azmon, A., Faes, C., Hens, N. (2013). On the estimation of the reproduction number on misreported epidemic data. Statistics in Medicine, 33(7):1176-1192. https://onlinelibrary.wiley.com/doi/abs/10.1002/sim.6015.
Zal het SARS-CoV-2 virus spontaan verdwijnen zodat we ons eigenlijk minder zorgen moeten maken?
Niets is minder waar, dit virus zal blijven. De vier coronavirussen die bij de mens vooral milde symptomen (zoals een bepaalde percentage van de verkoudheden) veroorzaken zijn na hun introductie evenmin verdwenen. Neem bijvoorbeeld het humaan coronavirus OC43, dat allicht al rond 1890 vanuit dieren op de mens werd overgedragen, circuleert vandaag nog steeds. Het enige coronavirus dat wel verdwenen is, is het SARS-CoV-1 dat in 2003 in Hong Kong aanleiding gaf tot een uitbraak. Echter, de reden voor het feit dat SARS-CoV-1 verdwenen is, is de efficiënte test & tracing, destijds gekoppeld aan strikte quarantainemaatregelen. Ook het pandemische influenza H1N1 virus, dat in 2009 de “Mexicaanse griep” veroorzaakte, is niet “verdwenen”. Licht gewijzigde varianten van dit virus circuleren nog iedere winter en eisen heel wat mensenlevens. Dat is overigens ook de reden waarom de Wereldgezondheidsorganisatie terecht onderdelen van dit virus opneemt in het jaarlijkse wintergriepvaccin. Misschien wel het meest tot de verbeelding sprekend is het Human Immunodeficiency Virus (HIV), de aanleiding voor het Acquired Immunodeficiency Syndrome (AIDS). Dit virus, dat ergens begin 1900 is ontstaan door overdracht van een virus van apen op de mens en pas in 1983 werd ontdekt, circuleert vandaag nog altijd. Het heeft ondertussen 35 miljoen slachtoffers geëist; naar schatting zijn nog ongeveer 30 miljoen mensen geïnfecteerd met dit virus.
Kan het viraal materiaal van het coronavirus binnendringen in het DNA van de cel?
Iedere familie van virussen heeft een eigen en heel specifieke manier van vermenigvuldigen. Voor ieder virus geldt wel dat nieuwe virusdeeltjes worden aangemaakt in de cellen van de gastheer. Voor het SARS-CoV2 is dat voornamelijk, maar niet uitsluitend, in de cellen van de luchtwegen en longen. Het genetisch materiaal van coronavirussen bestaat uit RNA. Het kan niet worden ingebouwd in het DNA van de cellen van de gastheer. HIV daarentegen, wat een volledig ander virus is, bouwt zijn genetisch materiaal wel in in het DNA van de gastheer. Om te begrijpen hoe vaccins en therapie kunnen ontwikkeld worden, is een zeer grondige kennis van de biologie van virussen vereist.
Waarom kon men in 2009 wel op enkele maanden tijd een vaccin klaar hebben tegen het H1N1 influenza virus (de “Mexicaanse griep”) en duurt het nu zeker anderhalf jaar voor er een vaccin is tegen SARS-CoV-2?
Ieder jaar zien we een piek van de wintergriep, doorgaans begint deze na nieuwjaar. Tegen de wintergriep begint men doorgaans in oktober te vaccineren. Griepvirussen muteren ieder jaar een klein beetje, vandaar dat men ook ieder jaar het griepvaccin lichtjes moet aanpassen. Heel soms, zoals met de grieppandemieën van 1918, 1958, 1968 en 2009, verandert het virus echter drastisch. Op basis van informatie over welke stammen in de winter in het Zuidelijk halfrond circuleerden (waar het winter is als het bij ons zomer is) beslist de Wereldgezondheidsorganisatie al in januari welke griepstammen zullen worden opgenomen in het vaccin waarmee men in de herfst gaat vaccineren. De methoden om het influenzavaccin te maken zijn heel goed gekend, men kan daar dus ieder jaar naar teruggrijpen. Ook voor het pandemisch H1N1 griepvirus van 2009 kon men zich gelukkig baseren op de bestaande kennis en methoden voor het maken van een vaccin. Daardoor had men op enkele maanden het vaccin tegen dit nieuwe griepvirus klaar, na het uitvoeren van de nodige klinische vaccinstudies. Coronavirussen behoren echter tot een volledig andere familie dan de griepvirussen (het griepvirus behoort tot de familie van de “orthomyxovirussen”). Gezien er nog geen vaccins bestaan tegen coronavirussen moet al die kennis en kunde nu in sneltempo worden opgebouwd. Doorgaans duurt de ontwikkeling van een vaccin vele jaren, het feit dat de eerste vaccins al in de loop van 2021 worden verwacht (pakweg 1 ½ jaar na het verschijnen van het virus) is een huzarenwerk, en is mogelijk omdat de vaccinontwikkelaars kunnen vertrekken van bestaande vaccinconstructies.