We baseren we ons hier op de dagelijkse cijfers van de bevestigde COVID-19 infecties per provincie van Sciensano. Het 7-daagse gemiddelde over de tijd middelt de verschillen en fluctuaties in testen en rapportering tijdens de week en het weekend uit, en is een manier om een meer robuuste curve te verkrijgen. Om dieper in te gaan op de onderliggende trends, berekenen we hier de groei over een periode van 21 dagen. Per definitie stijgt het aantal besmettingen in een populatie exponentieel indien geen beperkende maatregelen genomen worden, en bijgevolg kunnen we dit proces over de tijd voorstellen als:

geobserveerde besmettingen (tijdstip t) = geobserveerde besmettingen (tijdstip 0) * 10 $^{\textit{groeisnelheid x t}}$

of

geobserveerde besmettingen (tijdstip t) = geobserveerde besmettingen (tijdstip 0) * groeifactor $^t$.

Dit kunnen we ook uitschrijven als:

• geobserveerde besmettingen (dag 0) = geobserveerde besmettingen (dag 0) * groeifactor $^0$
• geobserveerde besmettingen (dag 1) = geobserveerde besmettingen (dag 0) * groeifactor $^1$
• geobserveerde besmettingen (dag 2) = geobserveerde besmettingen (dag 0) * groeifactor $^2$
• geobserveerde besmettingen (dag 3) = geobserveerde besmettingen (dag 0) * groeifactor $^3$
• …

De groeisnelheid kunnen we berekenen als de helling van de lineaire regressielijn gegeven door:

$Y_t$ = log10(geobserveerde besmettingen(t) +1) = $\beta_0$+ $\beta_1$ t + $\epsilon$,

waarbij $\beta_0$ gerelateerd is aan het aantal besmettingen op tijdstip 0 en $\beta_1$ de groeisnelheid aangeeft. De storingstermen $\epsilon$ worden verondersteld normaal verdeeld te zijn. Om ervoor te zorgen dat de uitkomstvariabele geen oneindige waarde aanneemt (want log10(0) = -$\infty$) werken we met een getranslateerde versie van het originele aantal besmettingen. Dit heeft een zeer beperkte invloed indien het aantal geobserveerde gevallen groot genoeg is.

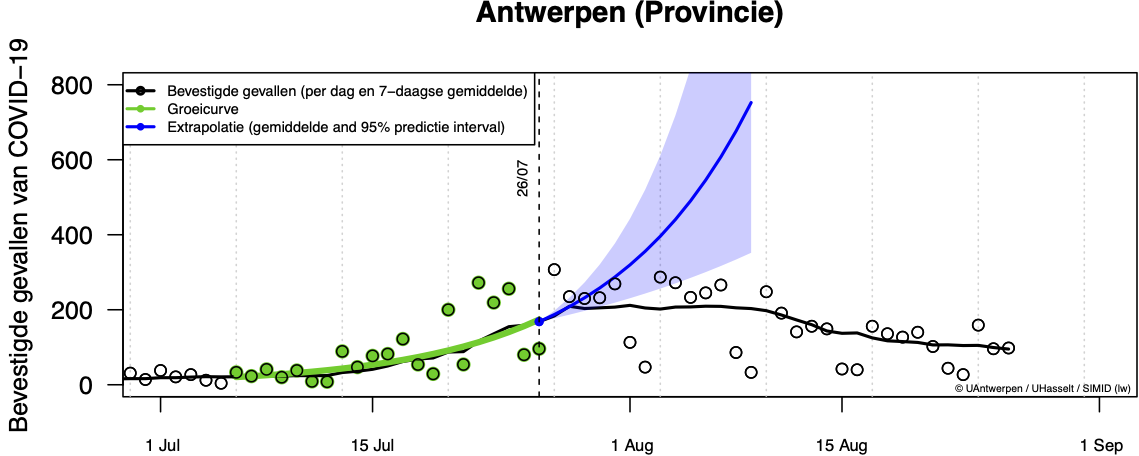
Ter illustratie van bovenstaande vergelijkingen geeft de volgende figuur de bevestigde COVID-19 gevallen weer voor de provincie Antwerpen vanaf 1 juli 2020 (zwarte cirkels) met een groeicurve (groen) op basis van de geobserveerde gevallen over 21 dagen. Indien we de geobserveerde groeifactor toepassen op het gemiddeld aantal bevestigde gevallen gedurende 7 dagen voor 26/7, krijgen we de weergegeven extrapolatie (blauw) met een gemiddelde evolutie en het 95% predictie interval. De meerwaarde van de groeicurve en de bijhorende extrapolaties zit voornamelijk in de vergelijking met de geobserveerde gevallen. Indien de extrapolaties niet overeenkomen met de werkelijkheid, wijst dit op een wijziging in de verspreiding en transmissie. De groeicurve gaat per definitie uit van een ongewijzigde groei (of afname) van het aantal bevestigde gevallen.

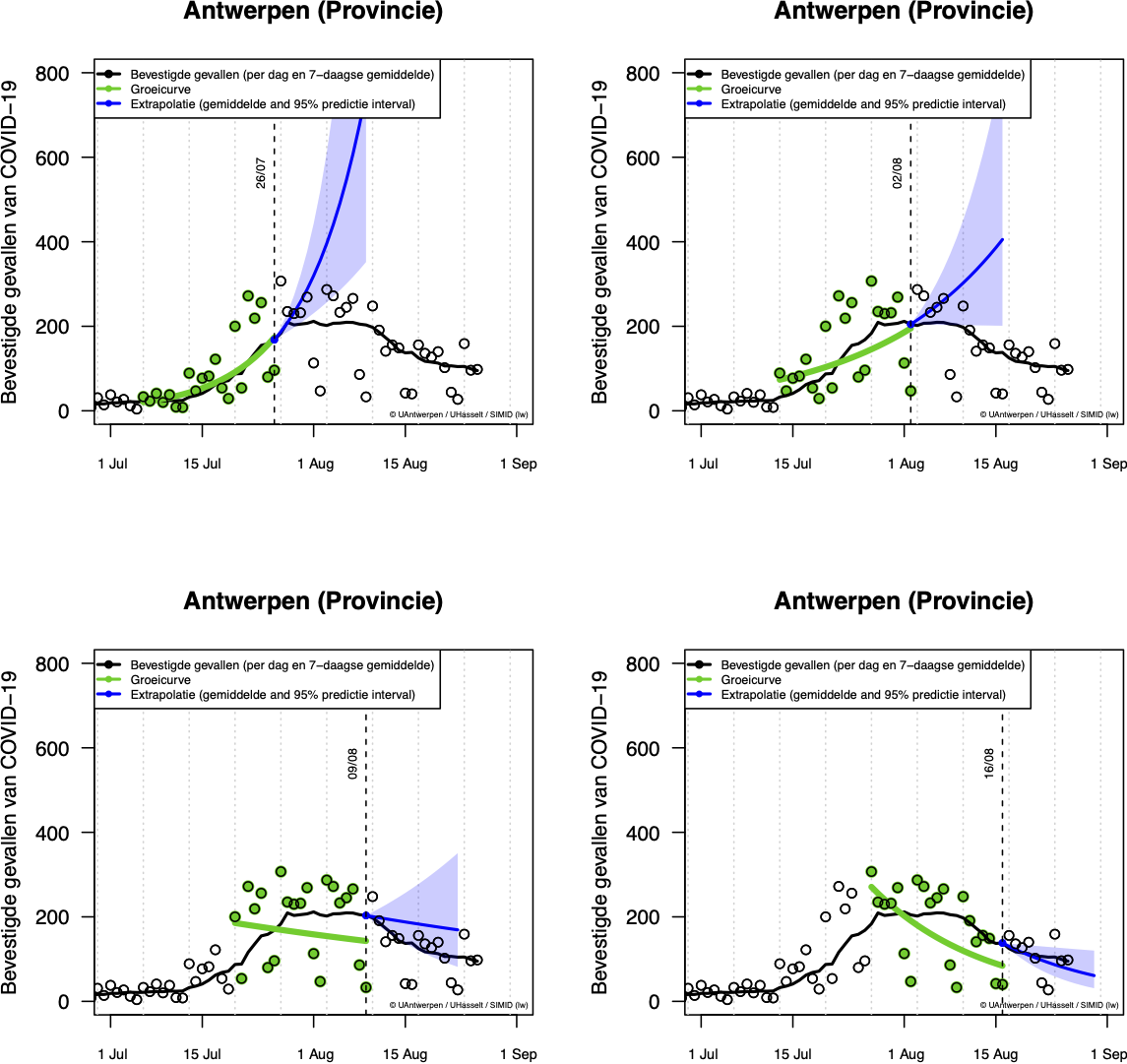
De volgende figuur geeft het aantal bevestigde gevallen van COVID-19 en het 7-daagse gemiddelde weer voor de provincie Antwerpen met de groeicurve op 4 momenten in juli-augustus 2020. De groei die we observeren tot 26/7/2020 wordt duidelijk niet voortgezet begin augustus. Er is een zeer groot verschil tussen de extrapolatie, die uitgaat van een ongewijzigde verspreiding, en de geobserveerde trends. De sterke stijging eind juli werd omgebogen tot een plateau om vanaf 9/8 terug te dalen. De 95% predictie intervallen bevatten het 7-daagse gemiddelde van de gerapporteerde gevallen behalve voor extrapolaties op 26/7. Dit duidt op een zeer drastische wijziging van de verspreiding.

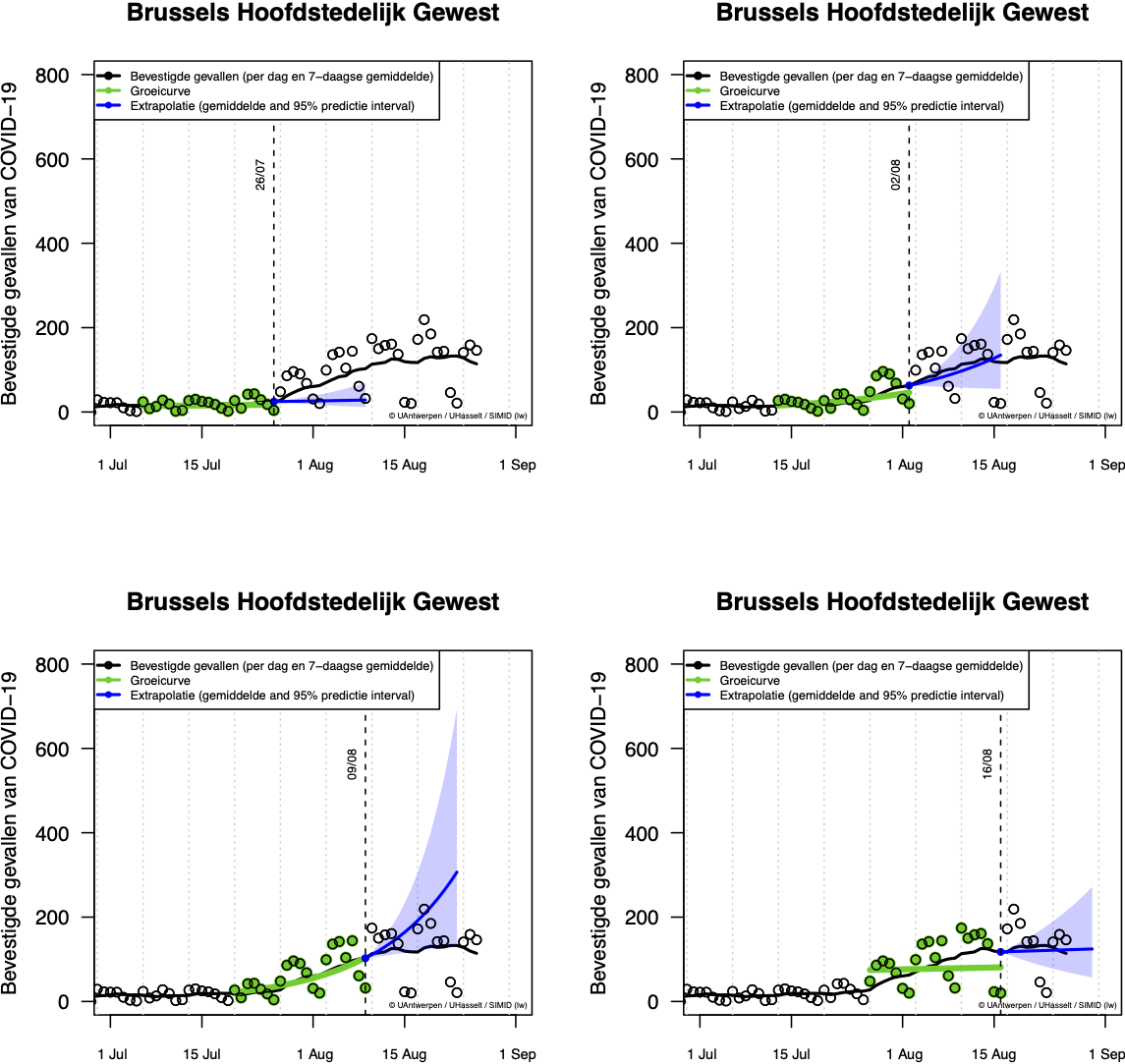
Voor het Brussels Hoofdstedelijk Gewest zijn de trends anders. De stijgende trend is pas duidelijk vanaf 26/7/2020. Tot en met de week van 10 augustus 2020 volgen de observaties de extrapolaties, en kunnen we spreken van een constante groei. Na dit punt, wijkt het geobserveerde aantal besmettingen af van de extrapolatie en observeren we een plateau. De laatste inschatting van de groeicurve volgt het plateau met een breed 95% predictie interval. De komende dagen en weken zullen ons leren of dit plateau slechts tijdelijk was of de voorbode van een afname.

Q&A:

Kan een stijging van het aantal COVID-19 testen ook de afwijking van de groeicurve verklaren? Meer testen betekent dat meer gevallen opgespoord kunnen worden. Indien men hierdoor meer positieve gevallen identificeert, zal dit de vergelijking met de groeicurve beïnvloeden. Maar indien het aantal testen stijgt en de geobserveerde trends nog steeds onder de extrapolaties liggen, bevestigt dit des te meer de afgenomen verspreiding als gevolg van aanpassingen in sociale interacties en/of toegenomen (hand)hygiëne.

Wat als de groei niet exponentieel maar sub-exponentieel is? In dit voorbeeld willen we de kwalitatieve verschillen aantonen op korte termijn door de extrapolatie te vergelijken met de geobserveerde trends. Het verschil met sub-exponentieel groei komt vooral op langere termijn tot uiting.

Kan je de groeicurve ook berekenen op een langere/kortere periode? Een groeicurve op basis van 14 dagen zal gevoeliger zijn om wijzigingen in de trends op te sporen, maar is ook meer onderhevig aan verschillen en fluctuaties in testen en rapportering. Voor dit voorbeeld hebben we een periode van 21 dagen gekozen om het evenwicht te bewaren tussen het kunnen oppikken van signalen en toch niet te gevoelig zijn voor kleine schommelingen.

Bronnen:

• Epistat website
• Anderson RM, May RM. Infectious diseases of humans. Oxford University Press; Oxford: 1991
• Comparative estimation of the reproduction number for pandemic influenza from daily case notification data. Chowell G, Nishiura H, Bettencourt LM, J R Soc Interface. 2007 Feb 22; 4(12):155-66.